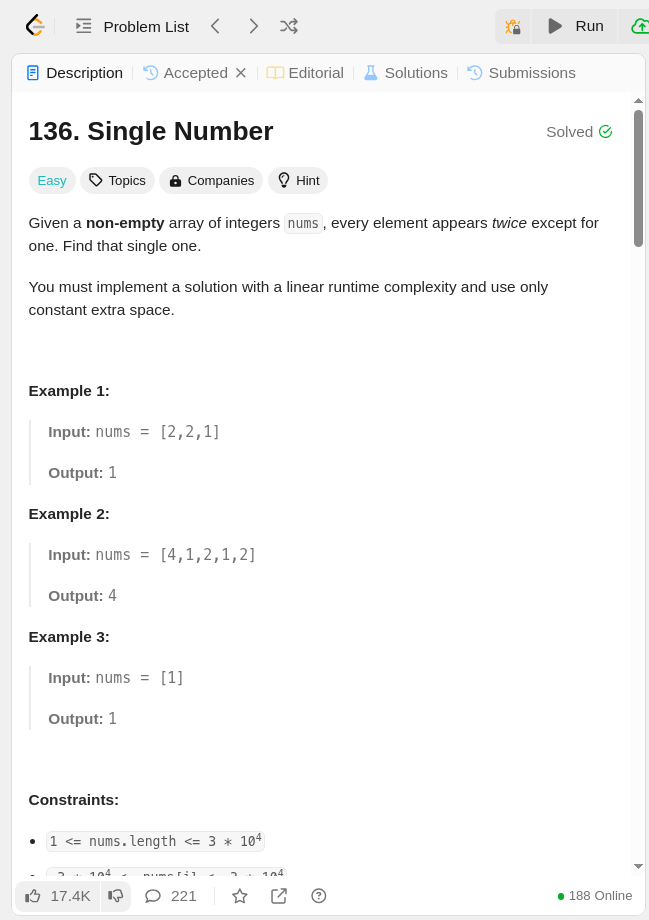
문제 설명
Single Number 문제는 정수 배열 nums가 주어졌을 때, 딱 한 번만 나타나는 숫자를 찾아내는 거임. 배열에 있는 숫자는 보통 두 번씩 나타나는데, 오직 하나만 한 번 등장함. 예를 들어:
- nums = [2,2,1] → 1이 답 (2는 두 번, 1은 한 번).
- nums = [4,1,2,1,2] → 4가 답 (1과 2는 두 번, 4는 한 번).
- nums = [1] → 1이 답 (한 개뿐이니까).
제약 조건:
- 배열 길이는 1 이상.
- 추가 메모리(공간복잡도)를 최소화하는 게 좋음. 즉, O(1) 공간으로 풀라는 힌트 같은 거임.
- 시간복잡도는 O(n) 정도로 풀어야 효율적임.
문제를 푼 과정
- 특이 케이스 처리
- 배열 길이가 1이면 바로 nums[0] 리턴함. 이건 한 번만 등장하는 숫자가 그거 하나뿐이란 뜻이니까 당연함.
- 코드에서 if len(nums) == 1 { return nums[0] }로 깔끔하게 처리했음.
- XOR 연산으로 해결
- tmp 변수를 0으로 초기화하고, 배열을 순회하면서 모든 숫자를 tmp에 XOR(^) 연산함.
- 예를 들어, nums = [4,1,2,1,2]면:
- tmp = 0 ^ 4 = 4
- tmp = 4 ^ 1 = 5
- tmp = 5 ^ 2 = 7
- tmp = 7 ^ 1 = 6
- tmp = 6 ^ 2 = 4
- 마지막에 tmp는 4가 됨. 이게 답임.
처음엔 2중 반복문으로 풀려다가 XOR로 바꿨는데, 2중 반복문은 시간복잡도가 O(n^2)까지 갈 수 있어서 비효율적임.
어떤 알고리즘 썼는지
- XOR 연산
- XOR의 성질이 이 문제 딱 맞음
- 같은 숫자끼리 XOR하면 0이 됨: a ^ a = 0.
- 0이랑 어떤 숫자 XOR하면 그 숫자 그대로: 0 ^ a = a.
- XOR는 교환법칙/결합법칙 성립: a ^ b ^ a = (a ^ a) ^ b = 0 ^ b = b.
- 그래서 배열의 모든 숫자를 XOR하면, 두 번 등장한 숫자는 0이 되고, 한 번 등장한 숫자만 남음.
- 시간복잡도: O(n) (배열 한 번 순회).
- 공간복잡도: O(1) (tmp 하나만 쓰니까).
- XOR의 성질이 이 문제 딱 맞음
- 선형 순회
- 배열을 한 번 쭉 돌면서 XOR 계산함. 별다른 자료구조 안 썼음.
- 이게 가능한 이유는 XOR이 메모리 없이 누적 계산으로 답을 뽑아낼 수 있어서임.
package main
import (
"os"
"fmt"
"bufio"
)
var (
wr = bufio.NewWriter(os.Stdout)
rd = bufio.NewReader(os.Stdin)
)
func singleNumber(nums []int) int {
if len(nums) == 1 {
return nums[0]
}
tmp := 0
for i := 0; i < len(nums); i++ {
tmp = tmp ^ nums[i]
fmt.Fprintln(wr, tmp)
}
return tmp
}
func main() {
defer wr.Flush()
singleNumber([]int{4, 1, 2, 1, 2})
}'leetcode , 백준' 카테고리의 다른 글
| [재귀,반복문] LeetCode 145번 문제 학습 (0) | 2025.04.15 |
|---|---|
| [재귀,반복문] LeetCode 141번 문제 학습 (0) | 2025.04.14 |
| [반복문] LeetCode 125번 문제 학습 (0) | 2025.04.11 |
| [반복문] LeetCode 121번 문제 학습 (0) | 2025.04.11 |
| [반복문] LeetCode 119번 문제 학습 (0) | 2025.03.21 |